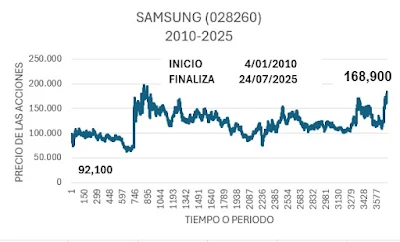
El estudio histórico del
comportamiento del precio de Samsung desde 2010 hasta 2025 (largo plazo) revela
patrones interesantes que merecen una atención cuidadosa.
La ecuación de la recta de
mínimos cuadrados es y=5.3746x+109082, con un coeficiente de determinación R2
de 0.06. La correlación del 24.52% es baja, lo que indica que esta línea solo
explica una pequeña parte de la variabilidad del precio. Sin embargo, sugiere
una leve tendencia alcista en el largo plazo. Es crucial entender que, si bien
la tendencia general es al alza, esta pendiente mínima no captura la
volatilidad ni los ciclos del mercado.
La polinómica de orden 6
(Verde), con una correlación del 67.51%, se ajusta mucho mejor a los datos,
explicando una parte significativa de la variabilidad del precio. Esta
polinómica es muy útil para identificar los ciclos del mercado. La observación
de que "empieza a descender el ciclo lo que indica que el precio va a
tener en el corto plazo un ajuste una disminución o descenso" es muy
pertinente. Una caída después de un pico en un ciclo de largo plazo sugiere una
corrección en el precio.
La polinómica de orden 3
(Morada), Con una correlación del 53.89%,también ofrece una mejor explicación
del comportamiento del precio que la recta de mínimos cuadrados, aunque no tan
precisa como la de orden 6. Ambas polinómicas (verde y morada), a pesar de sus
diferentes órdenes, son esenciales para visualizar los patrones de ascenso y
descenso en el mercado.
Los
pronósticos de 129,483.79 a 90 días y 129,967.50 a 180 días, estimados con la
ecuación de la recta de mínimos cuadrados y un nivel de confianza del 95%, son
útiles para obtener una proyección lineal.
nivel de confianza del 95%, significa que, si
repitiéramos este proceso de pronóstico múltiples veces, esperaríamos que el
valor real del precio caiga dentro de este rango el 95% de las veces.
Es fundamental reconocer que
la baja correlación de la recta (24.52%) implica que estos pronósticos son estimaciones
de tendencia general y no capturan la volatilidad ni los ciclos del mercado,
los cuales están mejor representados por las polinómicas. Para pronósticos a
corto y mediano plazo donde los ciclos son relevantes, apoyarse únicamente en
la recta de mínimos cuadrados podría llevar a subestimar o sobrestimar los
movimientos reales del precio. La inclusión de los rangos de confianza, como el
95% que has calculado (755,343.324), aunque muy amplio, es un recordatorio de
la incertidumbre inherente a las predicciones.
El contraste entre la leve
tendencia alcista de la recta de mínimos cuadrados y los ciclos descendentes de
las polinómicas (especialmente la de orden 6) es una observación econométrica
clave:
La diferencia en los R2
de las diferentes regresiones (recta, polinómica de orden 3, polinómica de
orden 6) indica que el modelo lineal es insuficiente para capturar la
complejidad del comportamiento del precio de Samsung. Esto sugiere que el
proceso generador de datos (DGP) no es simplemente lineal.
Las regresiones polinómicas,
al tener una mejor bondad de ajuste, resaltan la presencia de ciclos de auge y
caída. La observación de que la polinómica de orden 6 "empieza a
descender" sugiere que el mercado podría estar entrando en una fase correctiva
o bajista en el corto plazo, independientemente de la tendencia alcista de
largo plazo. Esto es crítico para la toma de decisiones, ya que un inversor que
solo se fije en la tendencia lineal podría ser sorprendido por una caída.
El análisis demuestra la
importancia de distinguir entre el comportamiento de largo plazo (tendencia
general, quizás influenciada por factores fundamentales de la empresa) y el
comportamiento de corto a mediano plazo (influenciado por ciclos de mercado, sentimiento
del inversor, etc.). Las polinómicas son más útiles para el corto y mediano
plazo, mientras que la recta de mínimos cuadrados nos da una idea del rumbo
general.
Si se utilizan únicamente los
pronósticos basados en la recta de mínimos cuadrados, se corre el riesgo de un sesgo
de omisión de variables (en este caso, la variable implícita del ciclo de
mercado), lo que podría llevar a errores significativos en las expectativas.
La aplicación de un modelo
ARIMA (Auto Regressive Integrated Moving Average) o un análisis de series de
tiempo más robusto sería altamente pertinente y recomendable para complementar
o mejorar este estudio:
El primer paso en un análisis
ARIMA es determinar si la serie de precios es estacionaria. Es muy probable que
la serie de precios de Samsung no sea estacionaria (tendencia y
estacionalidad/ciclos). Habría que aplicar diferenciación (I de
"Integrated" en ARIMA) para hacerla estacionaria. Componente AR
(Autorregresiva): Un modelo ARIMA podría capturar la dependencia del precio
actual con respecto a precios pasados, lo cual es muy probable dada la inercia
del mercado. Componente MA (Media Móvil): También podría modelar los errores
pasados, capturando shocks que persisten en el tiempo. Los modelos ARIMA,
especialmente los estacionales (SARIMA), son excelentes para modelar patrones
cíclicos o estacionales que las polinómicas están intentando aproximar. Un
modelo ARIMA podría identificar la longitud de estos ciclos y su impacto en el
precio.
Un modelo ARIMA bien ajustado,
al considerar la dependencia temporal, la tendencia (diferenciación) y los
componentes cíclicos/estacionales, ofrecería pronósticos más precisos y
robustos que la simple extrapolación de la recta de mínimos cuadrados.
Para un análisis financiero
más completo, después de un modelo ARIMA, se podría considerar un modelo GARCH
(Generalized Autoregressive Conditional Heteroskedasticity) para modelar la
volatilidad del precio de Samsung, que es un factor crucial en la gestión de
riesgos y la valoración de opciones. Los modelos de series de tiempo permiten
identificar cuándo se producen shocks significativos y cómo persisten sus
efectos en el tiempo.
El análisis realizado es un
excelente punto de partida. La combinación de la recta de mínimos cuadrados con
las regresiones polinómicas proporciona una visión inicial valiosa sobre la
tendencia y los ciclos. Sin embargo, para obtener pronósticos más precisos y un
entendimiento más profundo de la dinámica del precio de Samsung, especialmente
con la presencia de ciclos marcados, la aplicación de modelos de series de
tiempo como ARIMA (y posiblemente GARCH) sería el siguiente paso lógico y más
potente desde una perspectiva econométrica. Estos modelos permitirían no solo
predecir con mayor fiabilidad sino también entender mejor la estructura
subyacente del comportamiento del precio de Samsung.


No hay comentarios:
Publicar un comentario