El análisis del comportamiento
histórico del precio de las acciones del Banco Nacional de Chile (SN) entre
2010 y 2025 revela una tendencia general al alza, aunque con fluctuaciones
cíclicas. Las regresiones polinómicas sugieren una posible corrección a la baja
en el corto plazo, a pesar de que la tendencia lineal proyecta un incremento
moderado. Los pronósticos a 90 y 180 días, basados en el modelo lineal, son
$98,00 y $99,00 respectivamente, con un nivel de confianza del 95%.
La media de $56,79, es el
precio promedio de la acción durante el período analizado. La mediana de $52,97,
es la mitad de los precios observados están por debajo de este valor. La moda de
$72,41, es el precio que se presenta con mayor frecuencia. La desviación estándar,
de $25,58. Indica una dispersión significativa de los precios alrededor de la
media. La varianza de $654,45, refleja la alta variabilidad del precio de la
acción.
El rango de $130,81 muestra la
diferencia entre el precio máximo ($148,51) y el mínimo ($17,70) es
considerable, lo que subraya la volatilidad. La curtosis de $1,08 valor
positivo, aunque cercano a 1, sugiere que la distribución tiene colas más
pesadas y picos más anchos que una distribución normal, lo que podría indicar
la presencia de valores extremos.
La asimetría de $1,12 indica que la distribución de los
precios está sesgada hacia la derecha, es decir, hay más observaciones con
precios bajos y una cola más larga hacia precios altos.
El nivel de confianza del 95% se
establece en 0,89%, lo que hace
referencia al intervalo de confianza,
que determina una medida de estabilidad.
La rentabilidad de 696,55%, indica una rentabilidad muy alta
sobre el periodo analizado, lo cual es un indicador positivo de la inversión a
largo plazo.
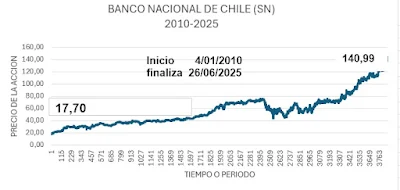
Las gráficas de "BANCO
NACIONAL DE CHILE (SN) 2010-2025" ilustran el comportamiento del precio de
la acción a lo largo del tiempo, con un precio inicial de $17,70 y un precio
final de $140,99. Se han superpuesto varias líneas de tendencia:
La recta de mínimos cuadrados
(Roja) con una correlación del 88,89%, esta recta muestra una leve tendencia al
alza en el precio de la acción a largo plazo. Su ecuación es y=0.0204x+17.399,
con un R2=0.7902. El alto coeficiente de determinación (R2)
sugiere que el modelo lineal explica una proporción significativa de la
variabilidad en el precio.
La polinómica de orden 6
(Verde), con una correlación del 97,85%, esta curva se ajusta muy bien a las
fluctuaciones históricas del precio. Es crucial la observación de que esta
línea "empieza a descender el ciclo", lo que sugiere un posible
ajuste, disminución o descenso del precio en el corto plazo. Esto indica que,
si bien la tendencia general es alcista, el mercado podría estar entrando en
una fase correctiva.
La polinómica de orden 3
(Morada), con una correlación del 93,94%, esta curva también captura el
comportamiento cíclico, aunque con un menor grado de ajuste que la de orden 6.
Ambas polinómicas (verde y morada) resaltan la naturaleza cíclica del mercado y
la posibilidad de un retroceso.
Los pronósticos a 90 y 180
días se basan en la ecuación de la recta de mínimos cuadrados (línea roja) y
los datos históricos, con un nivel de confianza del 95%:
Los pronóstico a 90 días de $98,00
y de 180 días de $99,00, enseñan el comportamiento futuro de la acción del
Banco Nacional de Chile.
Con el contraste de estas
tendencias, se pueden realizar las siguientes observaciones econométricas:
La coexistencia de una
tendencia lineal alcista robusta y patrones cíclicos marcados por las
regresiones polinómicas sugiere que el precio de la acción del Banco Nacional
de Chile es una serie de tiempo compleja que exhibe tanto tendencia como
estacionalidad/ciclicidad. La tendencia lineal (largo plazo) indica la
dirección general del movimiento del precio, mientras que las polinómicas
(medio a corto plazo) revelan las fluctuaciones inherentes al ciclo económico o
del sector.
Aunque la correlación de la
regresión lineal es alta, en un análisis de series de tiempo, es crucial
verificar si las series son estacionarias. Si el precio de la acción no es
estacionario (es decir, su media, varianza y autocorrelación no son constantes
a lo largo del tiempo), una regresión entre dos series no estacionarias puede
generar una correlación espuria. Esto no invalida la tendencia observada, pero
sí la interpretación de la significancia estadística de los coeficientes de
regresión sin un tratamiento adecuado de la no estacionariedad.
El hecho de que las
regresiones polinómicas (especialmente la de orden 6) muestren correlaciones
más altas que la lineal, indica que la relación entre el tiempo y el precio no
es puramente lineal. El mercado se mueve en ciclos, y los modelos no lineales son
más efectivos para capturar estos patrones de auge y caída. La señal de
descenso del ciclo en la polinómica de orden 6 es una observación econométrica
clave, ya que sugiere una desviación de la tendencia lineal de largo plazo en
el corto plazo, anticipando una corrección.
Con relación a la aplicación
del modelo ARIMA (AutoRegressive Integrated Moving Average) o análisis de
series de tiempo:
El modelo ARIMA sería una
herramienta extremadamente valiosa y apropiada para este tipo de análisis,
dadas las características observadas en los datos:
El primer paso en un análisis
ARIMA es determinar si la serie de precios es estacionaria. Si no lo es (lo
cual es muy probable para precios de acciones), se necesitará diferenciar la
serie (aplicar el operador 'I' de "Integrated" en ARIMA) para hacerla
estacionaria. Las visualizaciones gráficas de ciclos y tendencias sugieren no
estacionariedad en la media.
Una vez estacionaria, se
analizarían las funciones de autocorrelación (ACF) y autocorrelación parcial
(PACF) para identificar los órdenes de los componentes autorregresivos (AR) y
de promedio móvil (MA). Esto permitiría capturar la dependencia de los precios
actuales de los precios pasados (AR) y de los errores de pronóstico pasados
(MA).
Un modelo ARIMA, o más
específicamente un SARIMA si se detecta estacionalidad clara, es capaz de
modelar tanto la tendencia (a través de la diferenciación) como los patrones
cíclicos/estacionales observados. La regresión polinómica de orden 6 es una
buena indicación de la presencia de ciclos que un SARIMA podría modelar
explícitamente.
Un modelo ARIMA/SARIMA, al
considerar la estructura de dependencia temporal de los datos y su posible no
estacionariedad, generalmente produce pronósticos más precisos para series de
tiempo que los modelos de regresión simples, especialmente en el corto y
mediano plazo. Podría capturar mejor los puntos de inflexión y las fases de
contracción o expansión del ciclo.
Tras ajustar un modelo ARIMA,
se realiza un análisis de los residuos para asegurar que no contengan
información no capturada por el modelo (es decir, que sean ruido blanco). Esto
valida la idoneidad del modelo.
La aplicación de un modelo
ARIMA/SARIMA permitiría un análisis econométrico más riguroso y una capacidad
de pronóstico superior al capturar las complejidades de la serie de precios,
incluyendo su tendencia, estacionalidad y los componentes autorregresivos y de
promedio móvil, lo cual es fundamental para la toma de decisiones financieras.


No hay comentarios:
Publicar un comentario