MÁS ALLÁ DE LA TENDENCIA: UN ANÁLISIS PROFUNDO DE ULVR (2010-2025)

Unilever PLC opera como una empresa de bienes de consumo de alta rotación en Asia Pacífico, África, América y Europa. Opera a través de cinco segmentos: Belleza y Bienestar, Cuidado Personal, Cuidado del Hogar, Alimentos y Helados. Unilever PLC fue fundada en 1860 y tiene su sede en Londres, Reino Unido.

Los datos proporcionados cubren los precios históricos de las acciones de Unilever (ULVR) de 2010 a 2025, lo que representa un análisis a largo plazo.

Resumamos las estadísticas descriptivas clave del precio de las acciones de ULVR:

El precio medio es de aproximadamente 3435,31, con una mediana de 3800 y una moda de 2064. La diferencia entre la media, la mediana y la moda sugiere un grado de asimetría en la distribución.

La desviación típica de 969,55 indica una dispersión significativa de los precios en torno a la media. El rango de 3636 (de 1688 a 5324) subraya aún más la volatilidad de los precios durante el período.

La asimetría negativa de -0.27 indica que la cola izquierda de la distribución es ligeramente más larga o ancha. Esto sugiere que se han observado ganancias menores con mayor frecuencia o menos pérdidas importantes en comparación con una distribución perfectamente simétrica.

La curtosis negativa de -1.26 o (platicúrtica) sugiere que la distribución tiene colas más claras y un pico más plano que una distribución normal. Esto implica menos movimientos extremos de precios (tanto positivos como negativos) de lo que cabría esperar en una distribución normal.

Los valores de media, mediana, moda y desviación estándar (DE) son consistentes con las estadísticas descriptivas.

El valor "p" del 85,61% y el valor "q" del 14,39% se relacionan con la probabilidad de que el precio esté por debajo o por encima de un umbral determinado (posiblemente el valor "X" de 4466,00). Esto sugiere que el 85,61% de los precios observados fueron inferiores a 4466,00 y el 14,39% superiores.

El valor 'Z' de 1,06 indica a cuántas desviaciones estándar se encuentra el valor 'X' (4466,00) de la media.

El análisis presenta tres líneas de tendencia:

La regresión lineal (línea roja), cuya ecuación  y=0,7526 x+1955.7 y coeficiente de determinación de 0.776 define una correlación de 88.10%. La pendiente positiva de 0,7526 indica una ligera tendencia alcista en el precio de las acciones de ULVR a largo plazo (2010-2025). La alta correlación del 88,10 % sugiere una fuerte relación positiva entre el tiempo y el precio, lo que significa que el modelo lineal captura una parte significativa de la fluctuación del precio. R² de 0,776 confirma que aproximadamente el 77,6% de la variabilidad en el precio de las acciones puede explicarse por la tendencia lineal.

La regresión polinomial orden 6 (línea verde) con correlación de  96,38%, muestra una correlación muy alta, lo que indica un ajuste sólido a los datos históricos. La observación clave, como mencionó, es que el polinomio de orden 6 comienza a descender en su ciclo. Esto sugiere que, según este modelo más complejo, el precio podría experimentar un ajuste, una disminución o un descenso a corto plazo. Este modelo captura la naturaleza cíclica y los puntos de inflexión con mayor eficacia que el modelo lineal.

La regresión polinomial orden 3 (línea morada), que muestra una correlación de  92,77%, presenta una alta correlación, lo que indica un buen ajuste. Ofrece otra perspectiva del comportamiento del mercado, similar al polinomio de orden 6, al capturar patrones no lineales.

Los pronósticos a 90 días que da como resultado 4981.92 y el pronóstico de 180 días de 5049.66, con un

nivel de confianza: 95%, se basan en la ecuación de regresión lineal (línea roja) y el comportamiento histórico. La tendencia al alza en los pronósticos para 90 y 180 días coincide con la ligera tendencia alcista general que indica el modelo lineal. El nivel de confianza del 95 % implica que podemos tener una confianza del 95 % en que el precio real se mantendrá dentro de un rango determinado en torno a estos valores pronosticados.

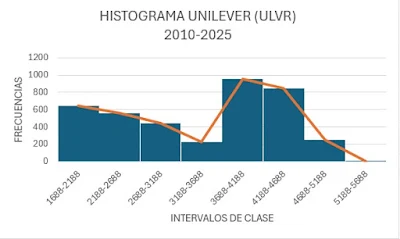
El histograma representa visualmente la distribución de frecuencia de los precios de ULVR en diferentes intervalos. La frecuencia más alta de precios parece estar en el intervalo 3688-4188, seguido por 3188-3688 y 2688-3188. Esta distribución visual confirma las estadísticas descriptivas, mostrando una concentración de precios alrededor del extremo superior de la distribución, con menos ocurrencias en los extremos inferior y superior.

La regresión lineal (correlación del 88,10 %) sugiere una tendencia alcista consistente, aunque gradual, a largo plazo en el precio de ULVR. Esto indica que, en promedio, la acción se ha revalorizado durante el período de 15 años. Desde una perspectiva econométrica, esto podría implicar que los factores fundamentales que sustentan el valor de la compañía han evolucionado positivamente.

Las regresiones polinómicas (especialmente las de orden 6) , con sus correlaciones más altas (96,38 % y 92,77 %), revelan la dinámica cíclica y no lineal de corto a mediano plazo que se superpone a la tendencia a largo plazo. La observación de que el polinomio de orden 6 comienza a descender es crucial. Esto significa que, si bien la tendencia fundamental subyacente podría ser positiva, el mercado se encuentra actualmente en una fase de corrección o consolidación. Este descenso en el ciclo sugiere que el precio probablemente se ha movido por encima de su valor fundamental o que existen presiones de mercado a corto plazo que provocan un retroceso.

Cuanto más alto R^2,  la correlación de los modelos polinómicos indica que capturan mayor varianza en el precio de las acciones que el modelo lineal simple. Esto representa una compensación econométrica: los modelos más complejos (como los polinomios de orden superior) pueden ajustarse mejor a los datos históricos al captar matices, pero podrían ser menos robustos para la predicción fuera de la muestra, especialmente si sobreajustan el ruido en lugar de los verdaderos patrones subyacentes.

El hecho de que el modelo lineal mantenga una fuerte correlación (88,10%) es importante. Esto sugiere que una parte significativa del movimiento de precios es genuinamente lineal, lo que representa una trayectoria de crecimiento fundamental. Los polinomios modelan las desviaciones en torno a esta trayectoria fundamental.

La naturaleza cíclica que representan las tendencias polinómicas, especialmente el descenso observado, podría interpretarse desde la perspectiva de la eficiencia del mercado. Si el mercado fuera perfectamente eficiente y siguiera un patrón aleatorio, estos patrones cíclicos claros serían menos predecibles. La presencia de estos ciclos sugiere períodos de sobrepasar y subpasar el valor intrínseco, lo que implica cierto grado de reversión a la media a corto y mediano plazo. Tras un período de movimiento alcista (como se observa en las primeras partes de las curvas polinómicas), un ajuste a la baja (el descenso actual) acerca el precio a su promedio o tendencia a largo plazo.

Los pronósticos del modelo lineal para 90 y 180 días (4981,92 y 5049,66) reflejan la continua trayectoria ascendente a largo plazo. Sin embargo, el contraste econométrico pone de manifiesto un posible conflicto: si el polinomio de orden 6 indica efectivamente un descenso a corto plazo, basarse únicamente en el pronóstico lineal podría llevar a una sobreestimación de los rendimientos a corto plazo.

Un enfoque de pronóstico econométrico más sólido implicaría combinar estos conocimientos: reconocer el sesgo alcista a largo plazo, pero también incorporar la fase cíclica actual. Esto suele llevar al uso de modelos que pueden capturar tanto los componentes tendenciales como los cíclicos/estacionales.

Dadas las observaciones, un modelo ARIMA (promedio móvil integrado autorregresivo) o un análisis de series temporales más amplio sería muy apropiado y proporcionaría conocimientos más profundos para ULVR:

El primer paso para aplicar un modelo ARIMA es verificar la estacionariedad. La presencia de una clara tendencia ascendente (aunque leve, como indica el modelo lineal) sugiere que la serie temporal no es estacionaria en media.

Probablemente necesitaríamos diferenciar la serie (p. ej., primera diferenciación) para que sea estacionaria. Esto implica transformar los datos en una serie de cambios de precios, en lugar de precios absolutos. El componente "Integrado" (I) de ARIMA aborda específicamente esta no estacionariedad mediante la diferenciación.

El ACF probablemente mostraría un decaimiento lento en la serie original, lo que confirma la no estacionariedad. Tras la diferenciación, el ACF revelaría los componentes de la media móvil (MA) (q).

El PACF ayudaría a identificar los componentes autorregresivos (AR) (p) del modelo. La presencia de ciclos en los ajustes polinómicos sugiere la posible presencia de propiedades autorregresivas significativas (es decir, los precios actuales dependen en gran medida de los precios pasados) y, potencialmente, componentes de media móvil (es decir, los errores actuales están relacionados con los errores pasados).

En función de la diferenciación requerida (d), y los patrones en los gráficos ACF y PACF, es posible identificar el modelo ARIMA(p,d,q) óptimo.

El comportamiento cíclico observado en los ajustes polinomiales podría sugerir la necesidad de un valor «p» o «q» de mayor orden para capturar estas oscilaciones. Por ejemplo, si los precios tienden a revertirse después de ciertos picos, esto sugiere un proceso autorregresivo.

Si bien el análisis actual no menciona explícitamente los patrones estacionales, un conjunto de datos de 15 años podría presentar estacionalidad (por ejemplo, patrones trimestrales o anuales relacionados con informes de ganancias, pagos de dividendos o ciclos de mercado más amplios). De ser así, un modelo ARIMA Estacional (SARIMA) sería aún más eficaz, ya que añade componentes estacionales (P, D, Q, S) al modelo ARIMA estándar.

Los modelos ARIMA están diseñados específicamente para pronosticar datos de series temporales. Una vez identificado y validado un modelo adecuado, este puede generar pronósticos precisos que consideran tanto la tendencia subyacente como los patrones cíclicos/autocorrelacionados identificados. Los pronósticos ARIMA probablemente brindarían una imagen más matizada que los pronósticos del modelo lineal, mostrando potencialmente la caída esperada a corto plazo sugerida por el polinomio de orden 6, antes de reanudar una tendencia ascendente.

Los modelos ARIMA manejan implícitamente la naturaleza secuencial de los datos de series de tiempo, a diferencia de los modelos de regresión estándar que suponen observaciones independientes (aunque existen modelos de regresión de series de tiempo).

Las regresiones polinómicas ofrecen un buen ajuste descriptivo, pero podrían no ser óptimas para la predicción de series temporales reales, ya que no consideran explícitamente los términos de error autocorrelacionados que suelen estar presentes en los datos financieros. ARIMA, al modelar los errores, puede proporcionar pronósticos estadísticamente más sólidos.

Si bien el análisis proporcionado proporciona una base sólida, especialmente con la visualización clara de tendencias y ciclos, un enfoque econométrico que utilice ARIMA o modelos de series temporales similares mejoraría la comprensión de la dinámica de precios de ULVR y la precisión de los pronósticos, en particular para las fluctuaciones de precios a corto y mediano plazo, al considerar formalmente la estacionariedad, la autocorrelación y la posible estacionalidad. El contraste entre la tendencia lineal simple y las complejas curvas polinómicas resalta la necesidad de modelos que puedan capturar tanto la dirección a largo plazo como las fluctuaciones inmediatas del mercado.